|
Geometri (eski adı Hendese) uzayı ve
uzayda tasarlanabilen şekilleri ve
cisimleri inceleyen matematik dalıdır.
Bu kelime Yunanca dır ve esas anlamı
yerin ölçülmesi demektir.
Geometri çok eski çağlardan beri vardır
ve sırasıyla Thales, Pisagor ve Eflatun
bu konu ile ilgilenmişlerdir.
Esas bilim haline gelmesi gene Yunanlı
olan Euclid ( M:Ö 330 M.Ö
275)sayesinde olmuştur ve EUCLID
GEOMETRİSİ OLARAK anılmaya başlamıştır.
Euclide, gelmiş geçmiş matematikçilerin
içinde adı geometri ile en çok
özdeşleştiren kişidir ve Geometrinin
babası olduğu söylenir.
Atina da Eflatunun akademisinde onun
talebesi olarak matematik öğrenimini
tamamlamış ve o dönemin en büyük şehri
ve aynı zamanda papirus endüstrisi ile
kitap ticaretinin merkezi olan
İskenderiye/ Mısıra gelmiştir.
Burada Elements/ Öğeler isimli 13
ciltlik bir kitap yazmış, uzay
geometrisini yeniden düzenlemiş ve
geometrinin sistemli bir ilim haline
gelmesine öncülük etmiştir. Euclide, bu
kitaplarda kendinden önceki Tales,
Pisagor, Eflatun, Aristoteles gibi
matematikçi ve geometricilerin
çalışmalarını temel olarak almış ve
kitapları yıllar boyu önemli bir başvuru
kaynağı olarak kullanılmıştır. Matbaanın
icadından sonra Elements kitabının 1000
defa baskısı yapılmış ve İncil den sonra
dünya üzerinde en çok satan kitap
olmuştur.
Düzlem geometrisi, aritmetik, sayılar
kuramı, irrasyonel sayılar ve katı
cisimler geometrisi Euclid in kitabında
ele aldığı başlıca konulardı.
Her önermeyi daha önceki önermelerden
çıkarma yöntemi kendisine atfedilen
geometrinin babası sözünü de haklı
kılar.
Euclid bilinen geometrik fikirleri basit
tanımlardan başlayıp daha sonra
aksiyomlara geçerek organize etmiş,
teoremleri belirlemiş ve mantıksal
ispatlar için metotlar ortaya koymuştur.
İspat edilen teoremlerden en önemlisi
Pisagor teoremidir.
Kitapta yer alan aksiyomlara (aksiyom:
ispata ihtiyaç duyulmadan kabul edilen
önermelerdir) teoremlere ve ispatlara
dayanan sentez yöntemlerinin Batı
düşüncesi üzerinde Kitabı Mukaddesten
sonra en etkili araç olduğu söylenir.
Euclidin ulaştığı sonuçlar her ne kadar
diğer matematikçiler tarafından da
belirtilmiş olsa da Euclid bu önerilerin
anlaşılabilir bir öğretici ve mantıklı
bir sisteme nasıl oturtulacağını
göstermiştir.
Euclid teoremlerini sunmak üzere
sentetik yaklaşım denilen bir metot
kullanmıştır. Bu metodu kullanarak kişi
bir dizi mantıklı basamaklardan
bilinenden bilinmeyene doğru bir gelişim
sağlar.
Elements/Öğeler kitapları günümüzde de
orta eğitimde okutulan düzlem geometrisi
ile başlar (ilk aksiyom sistemi ve
ispatların ilk örneği olarak).
Daha sonra üç boyutlu cisimler
geometrisi ile devam eder.
Einsteinın genel relativite teorisi
Euclid geometrisinin fiziksel boşluklar
ve düzlemlerin özelliklerini yansıtmak
için iyi bir araç olduğunu ancak
sağlıklı sonuçlar elde edebilmek için
çekim alanının çok güçlü olmaması
gerektiğini belirtmiştir.
Einstein Gençliğinde bu kitabın
büyüsüne kapılmamış bir kimse kuramsal
bilimde bir atılım yapabileceği hayaline
kapılmasın der. Euclide göre tabiat
kanunları tanrının matematiksel bir
düşünce şeklidir.
-Albert Einstein ise Şayet Euclid
sizin gençlik hevesinizi harekete
geçiremediyse o zaman siz bilimsel bir
düşünür değilsiniz demiştir.
-Dostoyevskinin meşhur kitabı
Karamazov kardeşler de romanın
kahramanlarından Ivan şöyle der
Size tanrı yı kabul ettiğimi
söylüyorum, ama şunu da belirteyim,
şayet Tanrı varsa ve hakikaten bu
dünyayı yarattı ise, hepimizin bildiği
gib Euclidin geometrisine göre
yaratmıştır.
İsimleri zamanımıza kadar uzanan
matematikçilerin, fizikçilerin astronomi
bilimi ile ilgilenenlerın İskenderi ye
de ki bu kültür merkezi ile çok yakında
ilgileri olmuştur. Daha sonraları
İslam âleminde de birçok matematikçiler
yetişti ve geometri üzerinde
çalışmalarına devam ettiler ve yeni
eserler verdiler.
Euclide Geometrisinin aksiyomları
şunlardır:
Aksiyom; İspata ihtiyaç duyulmadan kabul
edilen önermelerdir. Aksiyomlardan doğru
veya yanlış büyük ölçüde faydalanılır.
Doğru aksiyomlar doğru, yanlış
aksiyomlar ise yanlış sonuçların meydana
gelmesine sebep olurlar şunlardır:
Aynı şeye eşit olan şeyler birbirlerine
de eşittirler.
1.Eğer eşit miktarlara eşit miktarlar
eklenirse, elde edilenler de eşit olur.
2.Eğer eşit miktarlardan eşit miktarlar
çıkartılırsa eşitlik bozulmaz.
3.Birbirine çakışan şeyler birbirine
eşittir.
4.Bütün parçadan büyüktür.
EUCLIDEin postülatları şunlardır:
Postülat; Mantıki olarak doğruluğu kabul
edilmesine rağmen doğru veya yanlış
olduğu tespit edilemeyen önermelerdir.
Geometride postülatların kullanılması
bazı problemlerin çözümünde önemlidir.
- İki nokta bir doğru ifade eder
(herhangi iki nokta arasına bir düz
çizgi çekebilirsiniz, iki nokta arasını
birleştiren en kısa yol doğrudur)
-Doğru, doğru olarak sonsuza kadar
uzatılabilir
- Bir doğrudan bir doğru parçası elde
edilebilir
- Bir daire bir merkez ve yarıçapı ile
ifade edilir
-Bir dik açı bütünleyenine eşittir.
Bütün dik açılar birbirine eşittir.
- Bir doğru iki aykırı doğru tarafından
kesildiğinde meydana gelen iki açının
toplamı 180 dereceden küçüktür.
-
Bir üçgenin iç açıları toplamı 180
derecedir
Bir doğruya dışındaki bir noktadan
yalnızca bir tek paralel çizilebilir.
Düzlem geometride geometri uzayı iki
boyutlu düzlemdir. Euclid düzlem
geometrisinde temel elemanlar noktalar
ve doğrulardır. Teoremler matematik
aksiyomlardan yapılan çizimlerden sonuç
elde edilmesi şeklindedir. Euclide
geometrisinin en iyi bilinen ve
ispatlanmış teoremi Pisagor teoremidir.
Euclide geometrisi 19. yüzyılda ortaya
çıkan non euclide (euclide dışı)
geometriden yukarıda verilmiş meşhur beş
adet postülat ile ayrılır.
Bunlara ilaveten Euclid, 94 adet önerme
içeren Data isimli kitabını yazmış,
Küresel Astronomi ile ilgili olan
Phaenomena, aynalarla ilgili olarak
Caloptrics, perspektif teorisi ve
müzik teorisi üzerinde bir çalışma olan
Optics kitabını da yazmıştır. Optik le
ilgili çalışmasında Euclid ışın
huzmelerini geometrinin bir parçası
haline getirmiş ve onlarla sanki düz
çizgiymişler gibi uğraşmıştır.
Matematikte euclid geometrisinin çok
önemli ve temel bir yeri vardır. Aşağıda
uygulama alanı ile ilgili bazı resimli
örnekler verilmiştir.
|

Bir araştırmacı açık arazide
yatay ve dikey açıları,
uzaklıkları ölçmek için teodolit
kullanıyor. |

Yuvarlak cisim paketleme
prensipleri portakallara
uygulanıyor. |
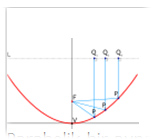
Parabolik bir ayna paralel ışık
huzmelerini odaklıyor. |
Kelimenin etimolojisinden de
anlaşılacağı üzere geometrinin ilk
başlardaki kullanılma amacı araştırma
yapmak içindi. Euclid geometrisinde en
temel ölçümler uzaklık ve açı ölçümleri
idi ve her iki ölçümde ispat edilmeden
çok evvel araştırmacı tarafından
yapılabiliyordu.
Yukarıda ortadaki resimde portakal
örneğinde görüldüğü gibi Euclid
geometrisinin uygulama alanlarından
biride ambalajlamadır. Örneğin kürelerin
en verimli bir şekilde n boyutta nasıl
yerleştirileceğini gösterir.
Geometrik optik mercekler ve aynalar
tarafından ışığın nasıl odaklandığını
analiz etmekte kullanılır.
|

Geometri sanat ve mimaride de
kullanılır. |

Buradaki su kulesi bir koni,
silindir ve yarım küreden
oluşmuştur. Hacmi kütle
geometrisi kullanılarak
hesaplanabilir. |

Geometri origami tasarımları
yapmak içinde kullanılır. |
Geometri ayrıca mimaride ve kağıt sanatı
olan origami de (kağıdı sadece
katlayarak hiçbir yapıştırma vs gibi
işlem kullanmadan şekiller yapma
sanatı) kullanılır.
Bazı klasik geometri problemleri pergel
ve gönye ile çözülemez, ama ancak
origami ile çözülebilir.
Euclid geometrisinin fiziksel uzayı
tarif ettiği iyice anlaşılmıştır. Ancak,
Einsteinın Genel rölativite teorisi
Euclid geometrisinin fiziksel uzayın
özellikleri için iyi bir yaklaşım
olduğunu ancak bunun içinde çekim
alanının çok güçlü olmaması gerektiğini
belirtir.
GÜNEŞ TUTULMASI DENEYİ

Yukarıdaki resim 1919 yılında bir güneş
tutulması sırasında çekilmiştir. Burada
yıldızlar küçük yatay çizgilerle
belirlenmiştir. Yıldızlardan gelen
dünyaya doğru gelen ışınlar güneşin
çekim gücünden dolayı eğilmektedir. Bu,
Einsteinın çekim gücü nedeniyle Euclid
geometrisinden sapmalar olacağı
öngörüsünü doğrulamaktadır.
Einsteinın genel relativite teorisi
uzay zamanın gerçek geometrisinin euclid
dışı geometri olduğunu göstermiştir.
Örneğin, üç ışık huzmesinden oluşan bir
üçgenin iç açıları toplamı çekim
gücünden dolayı 180 derece olmaz.
Günümüzde GPS sistemi yazılımlarında
Euclid dışı geometriler
kullanılmaktadır.
ABRAHAM LINCOLN ve Euclid ilişkisi
Abraham Lincoln 40 yaşında at sırtında
gezgin avukatlık yaparken akıl yürütme
de eğitici olması açısından Euclid le
ilgili çalışma yapmıştır ve onun
Elements/Öğeler isimli kitabını
sürekli olarak yanında taşımıştır.
O dönemde ortağı olan avukat yazmış
olduğu Lincoln biyografisinde onun gece
geç vakitlere kadar yerde gaz lambasının
ışığında Euclid geometrisi çalıştığını
anlatır.
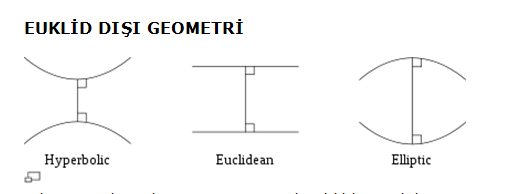
Dikey çizgilerin her üç geometri de
aldıkları şekil.
Euclid dışı geometride hiperbolic ve
eliptik geometrileri sayabiliriz.
Aralarındaki en büyük farklılık paralel
çizgilerle ilgili olandır.
İki boyutlu bir düzlemde sonsuza uzanan
düz çizgiler düşünün ve bunların her
ikiside bir üçüncü çizgi ile dik açı
yapsın.
Euclid geometrisinde çizgiler
birbirinden sabit bir uzaklığı korur ve
paralel çizgiler olarak adlandırılırlar.
Halbuki hiperbolik geometride bu
çizgiler birbirinden eğrilerek
ayrılırlar ve ortak dik açı ile
kesişme noktasından uzaklaştıkça
aralarındaki mesafe de artar.
Eliptik geometride ise bu çizgiler
birbirlerine doğru eğilir ve en sonunda
kesişirler.
Bunun en basit örneği bir küredir.
Aynen dünyamızda olduğu gibi birbirine
karşıt paralel veya meridyenler gibi
büyük daireler ve noktalar
özdeşleştirilirler.
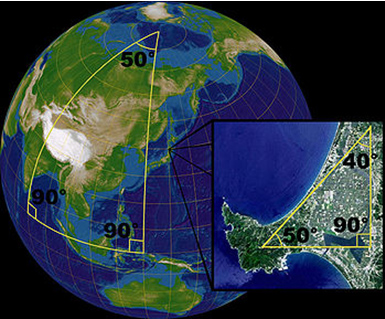
Aşağıdaki resimde görüldüğü gibi bir
kürenin üzerindeki bir üçgenin iç
açıları toplamı 180 derece değildir.
Kürenin yüzeyi Euclid uzayı değildir,
ancak lokalize olarak Euclid geometrisi
uygulanır.. Dünya düzlemi üzerindeki
küçük bir üçgende üçgenin iç açıları
toplamı 180 dereceye çok yakındır.
Euclid geometrisi bizim yassı bir
düzlem nosyonumuzu model alır.
 |