1. Fibonacci  (1170-1240)

Fibonacci orta çağların büyük matematikçilerindendir. İtalya’da Pisa’da doğmuştur.  Kuzey Afrika’da Berber Araplardan eğitim almış ve Akdeniz bölgesinde seyahat etmiştir. Bu gün kulandığımız1 2 3 4 5 6 7 8 9. ve 0 şeklindeki rakam dizinini Avrupa’ya “Liber Abbaci” adındaki kitabında öğretmiştir. Avrupalı matematikçiler bundan sonra ilk okulda öğretilen dört işlemi yapmaya ve  bu sistemi kullanmaya başlamışlardır.

Fibonacci serisi:

Her bir rakamın kendisinde önce gelen rakamla toplanması ile oluşturulan seriye Fibonacci serisi denir.  Deneyiniz: 1+1=2, 2+1=3, 3+2=5, 3+5=8  …………….vs :

 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181,

İşin insanı şaşırtan yönü bu serinin doğada kendisini sıkça göstermesidir: (Örneğin  Çiçekler, Deniz Kabukları, Bitkiler, Yapraklar vb) Öyle ki bu sanki önde gelen bir doğa yasası gibi görünür.

Birkaç örneğe bakalım:  

Çiçek Yaprakları (Taç Yaprakları)

Papatyalar da büyürlerken her dal Fibonacci serisine uygun yükselir

Şimdi Ay Çiçeğine bakalım:

İşler daha garipleşiyor: Eğer şekildeki modelde saat yönünde olan ve saat yönünün tersinde olan sarmalları sayarsanız Fibonacci serisindeki 21 ve 34 sayılarını elde edersiniz ki bu sayıların oranı “Altın Oran”dır. Şimdi bakalım doğada çok çok rastlanan bu Altın Oran ne?

Altın Oran:

Bir doğru parçasını iki parçaya bölelim: Bir parçası 1 birim diğer parçası x birim olsun.

Bu durumda 1 birim olan parçanın x birim olan parçaya oranı ile x birim parçanın tamamına oranı eşittir. Yani;

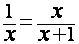
tir ve buradan altın oran sayısı bulunur:

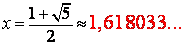
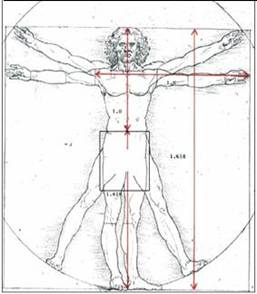
İnsan vücudunda Altın Orana verilebilecek ilk örnek; göbek ile ayak arasındaki mesafe 1 birim olarak kabul edildiğinde insan boyunun 1618'e denk gelmesidir.
Bunun dışında vücudumuzda yer alan diğer bazı “Altın Oran”lar şöyledir:

Parmak ucu-dirsek arası / El bileği-dirsek arası
Omuz hizasından baş ucuna olan mesafe / Kafa boyu
Göbek-baş ucu arası mesafe / Omuz hizasından baş ucuna olan mesafe
Göbek-diz arası / Diz-ayak ucu arası.

Parmaklarımız üç boğumludur. Parmağın tam boyunun ilk iki boğuma oranı altın oranı verir (baş parmak dışındaki parmaklar için). Ayrıca orta parmağın serçe parmağına oranında da altın oran olduğunu fark edebilirsiniz.

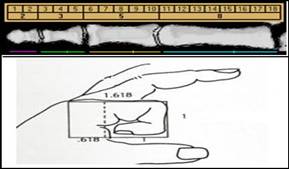
2 eliniz var iki elinizdeki parmaklar 3 bölümden oluşur. Her elinizde 5 parmak vardır ve bunlardan sadece 8'i altın orana göre boğumlanmıştır. 2 3 5 ve 8 Fibonacci sayılarına uyar.

İNSAN KOLUNDA

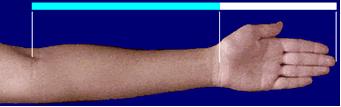
Şekilde görüldüğü üzere elimizin dirseğimizle bileğimiz arasında kalan bölgeye oranı 1618 dir. ( beyaz çizginin mavi çizgiye oranı )

İNSAN YÜZÜNDE ALTIN ORAN


İnsan yüzünde de birçok altın oran vardır. Ancak bunu elinize hemen bir cetvel alıp insanların yüzünde ölçüler almayı denemeyin. Çünkü bu oranlandırma bilim adamları ve sanatkarların beraberce kabul ettikleri "ideal bir insan yüzü" için geçerlidir. Örneğin üst çenedeki ön iki dişin enlerinin toplamının boylarına oranı altın oranı verir. İlk dişin genişliğinin merkezden ikinci dişe oranı da altın orana dayanır. Bunlar bir dişçinin dikkate alabileceği en ideal oranlardır. Bunların dışında insan yüzünde yer alan diğer bazı altın oranlar şöyledir:
Yüzün boyu / Yüzün genişliği
Dudak- kaşların birleşim yeri arası / Burun boyu
Yüzün boyu / Çene ucu-kaşların birleşim yeri arası
Ağız boyu / Burun genişliği
Burun genişliği / Burun delikleri arası
Göz bebekleri arası / Kaşlar arası.

Bunlar Mona Lisa tablosunda uygulanmıştır !!!

DNA'da Altın Oran

Canlıların tüm fiziksel özelliklerinin depolandığı DNA molekülü de altın orana dayandırılmış bir formda yaratılmıştır. DNA düşey doğrultuda iç içe açılmış iki sarmaldan oluşur. Bu sarmallarda her birinin, bütün yuvarlağın içindeki uzunluğu 34 angström, genişliği 21 angström'dür (1 angström; santimetrenin yüz milyonda biridir). 21 ve 34 art arda gelen iki Fibonacci sayısıdır, ayrıca 34/21  Altın Oranı verir.

Mimaride Altın Oran

Doğanın bu düzenini bilenler onu kullanmış ve ona uyan bir “ahenk” yaratmaya çalışmışlardır.

Leonardo da Vinci ve Corbusier tasarımlarını yaparken altın orana göre belirlenmiş insan vücudunu ölçü almışlardır.

İşte Böyle:

Türk mimarisi ve sanatı da altın orana ev sahipliği yapmıştır. Mimar Sinan'ın da birçok eserinde altın oran görülmektedir. Mesela Süleymaniye ve Selimiye Camileri'nin minarelerinde bu oran görülmektedir. Türk mimarisi ve sanatı da altın orana ev sahipliği yapmıştır: Konya'da Selçukluların inşa ettiği İnce Minareli medresenin taç kapısı, İstanbul'daki Davut Paşa Camisi, Sivas'ta Mengüçoğulları'dan günümüze miras kalan Divriği Külliyesi genel planlarından kimi ayrıntılarına dek altın oran kendini göstermektedir.


Eski Yunan Uygarlığında da altın dikdörtgen birçok yapıda kullanılmıştır. İ.Ö. 430 ve ya 440 yıllarında tanrıça Athena için yapılmış olan Partenon TAP, uzunluğu genişliğinin kök 5 katı olan bir dikdörtgen üzerine inşa edildiği anlaşılmaktadır. Ayrıca tapınakta daha başka altın dikdörtgenler de göze çarpmaktadır (altın dikdörtgen,kenarlarının oranı altın oran olan dikdörtgenlerdir).

Doğanın bu sırlarını bilen ve inceleyen Eski Mısırlılar piramitleri bu ölçülere uygun yapmışlar:karışık bir geometrik çözümdür Ama sonuçta her bir piramitin tabanının yüksekliğine oranı yine altın oranı veriyor.

Sırası gelmişken Piramitler hakkında azıcık bilgi verelim:

İşçilerin olağanüstü bir çabayla günde 10 metreküp taşı üst üste koyduklarını kabul edersek Keops piramidinde yer alan yaklaşık 2.5 milyon metreküp taş, 250.000 gün, yani yaklaşık 664 yılda yerleştirilebiliyor. Oysa piramitler 20 ila 30 yıl arasında bir sürede tamamlanmıştır.

Piramit dev bir güneş saatidir. Ekim ortasıyla Mart başı arasında düşürdügü gölgeler mevsimleri ve yılın uzunluğunu gösterirler.Piramiti çeviren taş levhaların uzunluğu bir günün gölge uzunluğuna eşittir.Bu gölgelerin taş levhalar üstünde gözlenmesiyle günün 0,2419 bölümünde yılın uzunluğu yanlışsız olarak saptanabilir.

Keops piramidinin yüksekliğinin 1 milyarla çarpımı yaklasık olarak güneşle dünyamız arasındaki mesafeyi verir. (149.504.000km)

Keops Piramidinin Taban çevresi, yüksekliğinin 2 katına bölünürse pi=3.14 sayı bulunur.

Piramitlerin üzerinden geçen meridyen karaları ve denizleri tam iki eşit parçaya böler.

Piramit, kimin adına yapıldıysa, onun bulunduğu odaya, yılda sadece 2 kez güneş girmektedir.

Bunlar da onun doğduğu ve tahta çıktığı günlerdir.

Piramitlerin içerisinde ultra sound, radar, sonar gibi cihazlar çalışmaz.

Gize'deki üç piramit aralarında bir Pisagor üçgeni olacak sekilde düzenlenmişlerdir.Bu üçgenin kenarlarının birbirlerine göre oranıi 3:4:5'dir.

Büyük Piramit'le dünyanin merkezi arasindaki uzaklık,Kuzey kutbuyla arasındaki uzaklığa eşittir ve ayrıca kuzey kutbuyla dünyanın merkezi arasındaki uzaklığa eşittir.

En son yeni tanıştığımız i-pod Nano’ya bakalım:

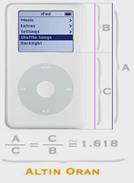
Bu yazı bir alıntıdır.
Derleyen: Nur Cihan