Kara Delik
Termodinamiği
Bu gelişmelerde merkezdeki oyuncu kara
deliktir. Kara delikler genel
izafiyetin, Albert Einsteinın 1915 teki geometrik çekim
teorisinin bir sonucudur.
Bu teoriye göre çekim uzay zamanın kıvrılmasından
kaynaklanmaktadır ve de cisimleri sanki bir kuvvet tarafından
çekiliyormuş gibi hareket ettirmektedir. Diğer yandan kıvrılma
da matter/kütle ve enerjiden kaynaklanmaktadır.
Einsteinın denklemlerine göre belirli bir derecede ve yeterli
yoğunluktaki bir kütle veya enerji uzay zamanı o denli güçlü
kıvıracaktır ki sonunda bir kara delik meydana getirecektir.
İzafiyet kanunları en azından fiziğin klasik tanımı çerçevesinde
(kuantum olmayan tanım) kara deliğin içine giren herhangi bir
şeyin dışarı çıkmasını kesinlikle yasaklamıştır . Geri dönüşü
olmayan noktaya (The point of no return) kara deliğin olay ufku
denir ve çok çok önemli bir noktadır. En basit şekli ile bu
ufuk bir küredir ve yüzey alanı kütle ağırlığı daha fazla olan
kara delikler için daha geniştir.
Kara deliğin içinde ne olduğunu tespit etmek imkansızdır. Hiçbir
detaylı bilgi ufuktan geçip dış dünyaya kaçamaz. Ancak,
ebediyen bir kara deliğe dönüşen bir kütle/matter bazı
izlerde bırakır. Kütlenin enerjisi (biz herhangi bir kütlenin
enerjisini Einsteinın E=mc2 formülüne göre tespit ediyoruz)
sürekli olarak kara deliğin kütlesinde bir increment****in
içinden yansıtılır.
Şayet, nesne deliğin etrafında dönerken yakalandı ise onun
açısal momentumu
kara deliğin angular momentumuna eklenir (veya
birleşir).
Kara deliğin hem kütlesi hem de
açısal momentumu
deliğin etrafındaki uzay zamana yaptıkları etki ile ölçülür.
Bu şekilde Law of conservation of energy
(enerjinin korunum ilkesi)
ve açısal momentum
kanunlarının doğruluğu kara delikler tarafından da teyit
edilir.
Ancak, görünüşe göre bir başka temel kanun, termodinamiğin
ikinci kanunu ihlal edilmektedir.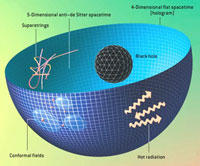
Termodinamiğin ikinci kanunu tabiatta ki proseslerin/işlem ve
olayların çoğunun
geri dönüşü olmadığını özetler. Şöyle ki bir çay fincanı
masadan aşağı düşer ve dağılır, ancak hiç kimse parçaların
kendiliğinden bir araya toplanıp yeniden birleşerek çay
fincanının yeniden oluşturduğunu görmemiştir. Termodinamiğin
ikinci kanunu bu şekilde inverse prosesleri/tersine işlemleri
yasaklar. Bu kanuna göre izole edilmiş fiziksel bir
sistemin entropisi hiç bir şekilde azalamaz. En iyi şekilde
entropi sabit kalır ve genelliklede artış gösterir. Bu kanun
fiziksel kimya (physical chemistry) ve mühendisliğin merkezidir
ve de fiziğin dışında, ancak fizik üzerinde büyük etkisi olan
bir fizik kanundur (fizik kanun olduğu tartışmalı bile olsa).
İlk olarak Wheeler tarafından üzerinde durulduğu gibi bir
nesne kara deliğin içinde kaybolduğu zaman onun entropisi
tamamen yok olur, böylece
termodinamiğin ikinci
kanunda geçersiz olur.
Bu bilmeceyi çözebilmek için ilk ipucu 1970 yılında ortaya
çıktı. O dönemde Demetrious Christodoulou (Princeton
Üniversitesinde Wheelerın yüksek lisans öğrencisi idi) ve
Cambridge Üniversitesinden Stephen W. Hawking birbirlerinden
bağımsız olarak çeşitli proseslerde
(matematiksel işlemlerle) örneğin kara delik
birleşmelerinde olduğu gibi olay ufuklarında hiç bir şekilde bir
azalma olmadığını ispatladılar.
Entropinin artması ile ilgili olarak yapılan analoji benim 1972
yılında şu öneriyi getirmeme neden oldu Kara deliğin entropisi
onun ufku ile orantılıdır). (Bkz.bir sonraki sayfadaki çizim) .
Benim düşünceme göre kara deliğin içine bir nesne/matter düştüğü
zaman kara deliğin entropisindeki artış her zaman bu nesnenin
kaybettiği entropiyi tamamlar, hatta gereğinden fazla tamamlar.
Daha genel olarak kara delik entropilerinin toplamı ve de kara
deliklerin dışındaki entropiler azalamaz. Kısaca bu
genelleştirilmiş ikinci kanundur.
Söz edilen bu genelleştirilmiş ikinci kanun çok sıkı, ancak
tamamen teorik testlerden geçmiştir. Bir yıldız kara delik
oluşturmak üzere çöktüğü zaman, kara deliğin entropisi yıldızın
entropisinin çok çok üzerindedir.
1974 yılında Hawking kara deliğin spontane olarak termal
radyasyon yaydığını bir quantum prosesi/işlemi yoluyla (Hawking
Radyasyonu olarak bilinen işlem) uygulamalı olarak göstermiştir.
(Bkz. The Quantum Mechanics of Black Holes, Stephen Hawking,
Scientific American, January 1977)
Bu fenomen karşısında Christodoulou-Hawking teoremi geçersiz
kalmaktadır (kara deliğin kütlesi ve de buna bağlı olarak ufuk
alanı azalmaktadır). Ancak, Genelleştirilmiş İkinci Kanun
bununla uyumludur: yayılan radyasyonun entropisi kara deliğin
decrementi içindeki entropiyi tamamlamaktan çok daha fazlasını
yapar, böylece genelleştirilmiş ikinci kanun muhafaza edilmiş
olur.
1986 yılında Syracuse Üniversitesinden Rafael D. Sorkin ufuğun
işlevini kullanarak kara deliğin içindeki bilgiyi bloke ederek
dışarıdaki olayları etkilemesini engellemiştir.
Böylece genelleştirilmiş ikinci kanun (veya ona çok
benzeyen başka bir şey) kara deliklerin geçirdiği inandırıcı
proses aşamaları için çok geçerlidir.
Onu argümanı şu olayı çok netleştirir: Genelleştirilmiş
İkinci Kanuna giren bir entropy X seviyesine inene kadar
hesaplanabilir.
Hawkingin radyasyon prensibi onun kara delik entropisi ile ufuk
entropisi arasındaki sabit değeri belirlemesini sağlamıştır.
Planck alanına göre (Planck uzunluğu 10-33 santimetre
kadardır ve yerçekimi ve quantum mekaniği ile ilgili en temel
ölçüdür. Planck alanı ise bu uzunluğun karesidir)ölçülen ufuk
alanının dörtte biri kara deliğin entropisidir.
Termodinamik olarak bile bu çok büyük bir entropi miktarıdır.
Bir santimetre çapındaki bir kara deliğin entropisi 1066 bit
tir, ki bu tek kenarı 10 milyar kilometre olan bir küp suyun
entropisine eşittir.
Hologram olarak Dünya
Genelleştirilmiş
ikinci kanun, bizim izole edilmiş herhangi bir fizik sisteme
sınırlar koymamıza izin vermektedir. Bu sınırlar X
seviyesine kadar olan bütün seviyelerdeki yapılardaki bilgiyi
kapsar.
1980 de ben bu sınırların birincisi üzerinde (evrensel entropy
sınırı olarak tanımlanmaktadır) çalışmaya başladım. Bu sınır,
ebadı belirlenmiş bir kütlenin ne kadar entropi taşıyabileceğini
belirler. (Yan sayfadaki kutuya bakınız).
Bununla ilişkili holografik sınır fikri, Stanford
Üniversitesinden Leonard Süsskind tarafından ortaya
atılmıştır. Bu sınır da uzayda belirli bir hacim kaplayan
matter/(madde)
ve enerjinin ne kadar entropi taşıyacağını belirler.
Holografik sınır ile ilgili çalışmasında Susskind, kara delik
olmayan, ancak küre şeklinde, izole edilmiş ve A olarak
tanımlanan, kapalı bir alanın içinde yerleşik olan bir
kütleyi incelemiştir.
Şayet kütle çöküp bir kara delik haline dönüşürse, ufuk alanı
A dan daha küçük olacaktır. Dolayısıyla, kara deliğin
entropisi A/4 ten daha kÜçüktür.
Genelleştirmiş İkinci Kanuna göre, sistemin entropisi azalamaz,
bu yüzden kütlenin orijinal entropisi A/4 ten daha
büyük olamaz.
Sonuç olarak A alanı ile sınırlanmış ve izole edilmiş bir
fiziki sistemin entropisi A/4ten daha küçük olacaktır.
Peki, kütle aniden ve
kendiliğinden çökmezse ne olacak? Ben, 2000 yılında
küçücük bir kara deliğin bütün sistemi bir kara deliğe
dönüştüreceğini belirttim ve bu söylem de Susskindin
argümanından çok farklı değildi. Dolayısıyla, sınır,
sistemlerin ana yapısından veya X seviyesinin özelliklerinden
bağımsızdır. O sadece Genelleştirilmiş İkinci Kanuna bağlıdır.
Biz, şimdi bilgi depolanmasının maksimum limitleri hakkındaki
soruları cevaplandırabiliriz.
Prensip olarak bir santimetreyi ölçen bir alet,1066
bite kadar tutabilir. Bu hayal edilmesi güç, şaşırtıcı
bir miktardır.
Gördüğümüz evrende en azından 10100 bit lik bir
entropi vardır. Prensip olarak bu miktar, çapı bir ışık yılının
onda biri olan bir kürenin içine yerleştirilebilir. Evrenin
entropisini hesaplamak zor bir problemdir ve çok daha
büyük sayılar, hatta, evrenin kendisi kadar büyüklükte bir
küreye gereksinme gösterecek kadar büyük sayılarında ortaya
çıkması mümkündür.
Ancak, esas şaşırtıcı olan, holografik sınırın başka bir
özelliğidir.
Kısaca söylemek gerekirse, olabilecek maksimum entropi hacim
yerine sınırlayıcı alana bağlıdır. Bir an bilgisayarın hafıza
chiplerini büyük bir yığın haline getirdiğimizi düşünelim.
Transistörlerin sayısı, toplam data depolama kapasitesi bu
yığının hacmi ile orantılı olarak yükselir. Aynı şekilde bütün
chiplerin toplam termodinamik entropisi de yükseliş gösterir.
Dikkâti çeken bir diğer nokta da teorik olarak, yığının
kapladığı boşluğun bilgi kapasitesi, sadece yüzey alanına bağlı
olarak yükseliş göstermektedir. Hacim, yüzey alanından daha
hızlı yükseldiği için belli bir noktaya gelince chiplerin
tamamının entropisi holografik sınırı aşacaktır.
Bu durumda ya Genelleştirilmiş İkinci Kanunun veya bizim entropi
ile ilgili sağduyulu fikirlerimizin geçersiz olması gerekir.
Gerçekte geçersiz olacak yığının kendisidir, çünkü daha bloke
olacağı noktayı bulmadan kendi çekiminin altında çökecek ve bir
kara delik oluşturacaktır. Bu aşamadan sonra ilave edilecek her
chip, kara deliğin kütlesini ve yüzey alanını Genelleştirilmiş
İkinci Kanunu koruyacak şekilde arttıracaktır. Bu sürpriz
sonuç, yani enformasyon kapasitesinin yüzey alanına bağımlı
olmasının son derece doğal bir anlatımı vardır. Bu doğal
anlatım, ancak holografik prensip doğru ise geçerlidir.
Bilindiği üzere holografik prensip 1993 yılında Hollanda/Utrecht
Üniversitesinden Nobel ödüllü Prof. Gerardt Hooft tarafından
ortaya atılmış ve Susskind tarafından geliştirilmiştir.
Günlük yaşamda bilinen hologram, çok özel bir fotoğraftır ve
eğer doğru bir şekilde aydınlatılırsa fotoğrafı çekilmiş nesne
her ne ise onun Üç boyutlu bir görüntüsünü verir. Bu Üç
Boyutlu görüntüyü tanımlayan/tarif ve tasvir eden bütün bilgi,
iki boyutlu bir film parçasının üzerindeki açık ve koyu renkli
desenlerin üzerine kodlanmıştır ve yeniden bir
biçim,
şekil almaya hazır
şekildedir.
Holografik prensibin son derece kesin olarak söylediği bir şey
vardır. Holografik sistem der ki: Bu görsel büyüde uygulanan
düşünce Üç boyutlu bir yer kaplayan her türlü sistemi fiziksel
olarak tasvir etmek ve tanımlamak için uygulanabilir. Bu
prensibin önerisine göre başka bir fizik teorisi sadece iki
boyutlu bölgenin sınırının üzerinde tanımlanmasına rağmen Üç
Boyutlu fiziği tasvir edebilir. Şayet Üç Boyutlu bir
sistem sadece onun İki Boyutlu sınırı üzerinde çalışan bir
fizik teorisi ile tanımlanabiliyorsa, o zaman sistemdeki
bilginin sınırdaki tanımlanmayı geçmeyeceği düşünülür.
Sınırı üzerine resmedilmiş bir Evren
Biz holografik
prensibi bütün evrene uygulayabilir miyiz? Esas evren Dört
Boyutlu bir sistemdir, hacmi vardır ve zamanla
genişlemektedir. Şayet bizim evrenimizin fiziği holografi ise,
o zaman alternatif bir takım fizik kanunları olacaktır ve bu
kanunlar bir yerlerde uzay zamanın Üç Boyutlu sınırı üzerinde
çalışacaklardır ve de bu bizim bildiğimiz Dört Boyutlu fiziğe
eş değer olacaktır. Şu anda henüz bu şekilde çalışan bir Üç
boyutlu teori bilmiyoruz. Gerçekte evrenin sınırı olarak hangi
yüzeyi kullanmamız gerekir? Bu fikirleri gerçekleştirebilmek
için atılacak bir ileri adım ise evrenimizden daha basit
modelleri incelemek olacaktır.
Holografik prensiple ilgili somut örnekler anti-de Sitter uzay
zamanlarını içermektedir. Orijinal de Sitter uzay zamanı
ve kozmolojik sabit (cosmological constant) olarak bilinen
repulsive force (itici kuvvet)
ile birlikte ilk defa Hollandalı astronom Willem de Sitter
tarafından 1917 yılında Einsteinın denklemlerine bir çözüm
olması amacı ile elde edilmiştir.
De Sitterin uzay zamanı boştur, gittikçe ivmesi artan bir
şekilde genişlemektedir ve çok yüksek bir simetrisi
vardır. 1997 yılında uzaktaki süpernova patlamalarını
inceleyen astronomlar, evrenimizin ivmesi gittikçe artan bir
şekilde genişlediğini ve gelecekte büyük bir ihtimalle
git gide de Sitter uzay zamanı gibi olacağı sonucuna
varmışlardır.
Şimdi, şayet Einsteinın denklemlerindeki
repulsion attraction= itici
güç çekim gücüne
döndüyse; de Sitterin çözümü anti-de Sitter uzay zamanı şekline
döner ve eşdeğer bir şekilde aynı simetriye sahiptir.
Holografik konsept için daha da önemli olan nokta ise bu uzay
zamanın bir sınırı vardır, bu sınır sonsuzda konumlanmıştır
ve bizim gündelik uzay zamanımıza çok benzemektedir.
Teorisyenler Anti-de-Sitter uzay zamanını kullanarak
holografik presibin çalışmasına somut bir örnek yapmışlardır.
Buna göre anti-de-Sitter uzay zamanı içinde fonksiyonel olan ve
superstring (süpersicim) teorisi
ile tanımlanan bir evren bu uzay zamanın sınırında
fonksiyonel olan bir kuantum alanı teorisine eşdeğerdir.
(Yukarıdaki kutuya bakınız)
Böylece, bir anti-deiSitter evreninde ki süperstring
(süpersicim) teorisi
evrenin sınırına resmedilmiştir.
1997 de Harvard Üniversitesinde olan Juan Maldacena o zaman ilk
defa Beş Boyutlu anti-de-Sitter vakası için böyle bir ilişki
olduğunu düşündü. Daha sonra Princeton, İleri Çalışmalar
Enstitüsüne mensup Edward Witten ve gene aynı üniversitede
Steven S. Gubser, Igor R. Klebanov ve Alexander M. Polyakov
tarafından teyit edildi. Bu holografik iletişimin örnekleri
şimdi çok değişik boyutlara sahip uzay zamanlar içinde
bilinmektedir.
Bu sonuç göstermektedir ki, çok farklı görünen iki teori aynı
boyutun uzay boşluğunda çalışmasalar dahi birbirinin
eşdeğeridir.
Bu evrenlerin herhangi birinde yaşayan mahluklar, kendilerinin
hangi evrende yaşadıklarını bilemeyeceklerdir; string teori
süpersicim
tarafından tanımlanan Beş Boyutlu bir evrende mi yoksa nokta
parçacıkların kuantum alan teorisi ile tanımlanan Dört Boyutlu
bir evrende mi yaşadıklarını tesbit edemeyeceklerdir. (Tabii
ki, onların beyin yapıları kendilerine sağduyu ya dayalı bir
önyargı verecektir. Bu ön yargıya göre de tanımlardan birisi
geçerli olarak kabul edilecektir, tıpkı beyinlerimizin
evrenimizin Üç Boyutlu olduğuna dair yaptığı bir algılama da
olduğu gibi. ( Örnek yan sayfadaki resim)
Holografik eşitlik Dört Boyutlu uzay zamanda zor bir hesap
işlemine yol açar, çünkü kuark ve gluonların davranışları
ve bunların birbirleri ile değiştirilmeleri (alışverişleri) söz
konusudur. Ancak, çok simetrik olan Beş Boyutlu anti-de-Sitter
uzay zamanda bu hesap daha kolaydır.
Bu eşdeğerlilik diğer taraftan da çalışır. Witten
göstermiştir ki, anti-De-Sitter uzay zamandaki bir kara delik
alternatif fizikte sınırlayan uzay zamanda üzerinde bulunan
kızgın radyasyona eşdeğerdir.
Deliğin entropisi son derece derin ve esrarengiz bir konu-
radyasyonun entropisine eşittir ve bu çok normaldir.
Genişleyen Evren
Yüksek oranda
simetrik ve boş olan Beş Boyutlu anti-de Sitter evreni Dört
Boyutlu olan, matter, radyasyon,ve pek çok zarar verici
şiddetli olayla dolu olan bizim evrenimize benzemez.
Biz kendi evrenimizi içinde matter/madde
ve uniform/düzgün bir şekilde dağılmış radyasyonu olan bir
evren gibi düşünsek de sonuçta gene bir anti-de-Sitter evreni
elde edemeyiz ve de daha çok Friedmann-Robertson-Walker
evreni elde ederiz.
Bugün pek çok kozmolojist evrenimizin bir Friedmann-Robertson-Walker
evrenine benzediği konusunda fikir birliğine varmıştır, yani
sonsuzdur, sınırı yoktur ve sonsuza kadar genişlemeye devam
edecektir.
Böyle bir evren holografik prensip veya holografik sınırla
uyumlu mudur?
Susskindin çökerek kara deliğe dönüşümle ilgili argümanı
burada bize yardımcı olamaz. Aslında, kara deliklerden ortaya
çıkarılan holografik sınırın düzenli bir şekilde genişleyen
evrende kırılması gerekir.
Matter/madde ve
radyasyonla dolu olan bir bölgenin entropisi gerçekten onun
hacmine orantılıdır. Dolayısıyla, yeteri kadar geniş bir bölge
holografik sınırı geçersiz kılacaktır.
1999 yılında o zaman Stanford Üniversitesinde olan Rafael Bousso,
modifiye edilmiş bir holografi sınır önermiş ve o günden beri
bunun daha evvel tartıştığımız sınırların uygulanamadığı
yerlerde bile uygulandığı görülmüştür.
Boussonun formülü herhangi bir İki Boyutlu yüzeyle başlar, bu
yüzey bir küre gibi kapanabilir veya bir sayfa gibi açılabilir.
Burada yüzeyin tek kenarından aynı anda ve dikey olarak fışkıran
ışık huzmeleri hayal edilir.
Yani talep edilen tek şey, başlangıç için aynı noktaya gelen
hayali şık huzmeleridir. Örneğin, küre şeklinde bir deniz
kabuğunun iç yüzeyinden yayılan ışık bu gereksinmeyi
karşılar. Daha sonra bu hayali ışık huzmelerinin kesişmeye
başladıkları noktaya kadar içinden/arasından geçtikleri matter/madde
ve radyasyonun entropisinin ne olduğu düşünülür.
Boussonun düşüncesine göre bu entropi esas ana yüzeyin temsil
ettiği entropiden daha fazla olamaz (Planck alanı birimine göre
ölçüldüğü zaman ilk alanın dörtte bir kadar).Bu entropi
hesaplaması, holografik sınırda kullanılan entropi hesap
metodundan daha farklıdır.
Boussonun sınırı bir yerdeki belli bir zamandaki entropiyi
belirtmez, onun belirttiği değişik zamanlardaki ve yüzeyden
fışkıran ışıkla aydınlanan yerlerdeki entropidir.
Boussonun sınırı kendi içine diğer entropi sınırlarını da dahil
eder, ancak onların kısıtlamalarından uzak durur.
Hem evrensel entropi hem de Gerardt Hooft-Susskind formundaki
holografik sınıra Boussonun holografik sınırından
ulaşılabilir. Boussonun
sınırı çok hızlı gelişmeyen ve çekim alanı (gravitational field)
çok kuvvetli olmayan herhangi bir izole sistem için de
geçerlidir.
Şayet bu şartlar aşılırsa -aynen kara deliği içinde çöken
bir matter/(madde)
küresinde olduğu gibi- o zaman bu sınırlar sonunda geçersiz
olur, ancak Boussonun sınırı geçerliliğini korur. Bousso
göstermiştir ki, onun stratejisi İki Boyutlu yüzeylerin
(üzerlerinde dünyanın hologramlarının kurulabileceği) yerlerini
tespit etmek içinde kullanılabilir.
Bir
Devrimin İşaretleri
Araştırmacalar
daha pek çok entropi sınırı önermişlerdir. Holografik motif
üzerindeki varyasyonların hızla artması göstermektedir ki, bu
konu henüz bir fizik kanun olma statüsüne erişmemiştir. Ancak,
holografik düşünce şekli tam olarak anlaşılmamasına rağmen,
burada kalacaktır. Aynı zamanda onunla birlikte elli
yıldır geçerli olan alan teorisinin fiziğin tek ve temel lisanı
olduğu görüşünden de vazgeçilmesi gerektiği idrak edilmiştir.
Alanlar, örneğin elektromanyetik alanlar bir noktadan diğerine
değişim gösterir ve böylece sonsuz
serbestlik dereceleri
tanımlarlar.
Holografi,sınırlanmış bir alan içinde mevcut
serbestlik derecelerini
sonlu bir sayıya indirger (finite number). Sonsuzluğu
ile birlikte alan teorisi en son oluş değildir. Bundan da öte
sonsuz eğitilebilse bile, yüzey alandaki bilginin esrarengiz
bağımlılığı mutlaka bir şekilde
yerleşik,
kalıcı olmalıdır.Holografi
daha iyi bir teoriye rehber olabilir. Temel teori nedir?
Holografiye bağlı olarak gelişen düşünceler zinciri bazı
kişilere değişik öneriler getirmiştir. Bunlardan en
belirgin olanı Waterloodaki Perimeter Institute for
Theoretical Physics mensubu Lee Smoline ait olandır. Buna
göre en son gelinen noktadaki teori alanlarla ilgilenmemeli,
hatta uzay zamanla da ilgilenmemeli, ama fiziksel
işlemler
arasındaki bilgi alışverişi ile ilgilenmelidir. Şayet
bu yapılırsa, dünyanın yapıldığı maddenin bilgi olduğu
şeklindeki vizyon/görüş
kendisine sağlıklı bir kılıf bulacaktır.
JACOB D: BEKENSTEIN kara delik termodinamiğinin temeline ve
bilgi ile çekimin (gravitation) diğer yönlerine değerli
katkılarda bulunmuştur.
Kendisi Kudüs İbrani Üniversitesinde Teorik Fizik Profesörü
olan bir Polonyalıdır. Aynı zamanda Israil Bilim ve İnsanlık
Akademisi üyesidir ve Rothschild ödülünü kazanmıştır.
Bekenstein bu makaleyi üç yıl önce kendisinin doktora danışmanı
olan John Archibald Wheelera ithaf etmiştir. Wheeler, Ludwig
Boltzmannın Üçüncü jenerasyon talebelerindendir. Wheelerın
doktora danışmanı Karl Herzfeld ise Boltzmannın talebesi olan
Friedrich Hasenöhrlün talebesidir:
İstanbul
- 07.10.2003
http://gulizk.com
Scientific American
August 2003 |